The composite internal dispersion is a measure of the variability of portfolio-level returns for only those portfolios that are included in the composite for the full year around the composite return. First, the firm must identify which portfolios were in the composite for the full year. Second, the firm must calculate the annual return for each of the portfolios that were included in the composite for the full year. The internal dispersion measure is then calculated using these portfolio-level annual returns. The specific measure of dispersion presented is a required disclosure. If the firm has less than five portfolios in a composite, a measure of dispersion is not required.
The GIPS standards do not require a specific formula for dispersion. A firm could present the standard deviation, a range (i.e., high and low), quartiles, or any other appropriate method of central dispersion.
We’ll use the weighted standard deviation as the dispersion calculation method. Standard deviation is a measure of variability that is often used in the investment industry as an indicator of risk. This statistic measures the variability (dispersion) of the asset weighted account return around the asset-weighted mean composite return. This measure can be annual or quarterly.
Equal weighted Standard deviation
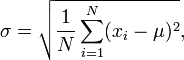
Where xi is return of portfolio i in year of calculation,
N is number of portfolios that are in composite for the full period,
and μ is the composite’s equal weighted return in period of calculation.
Asset weighted Standard deviation
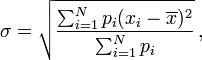
Where pi is the weight of portfolio i in composite
and 
is the composite’s weighted return in period of calculation.
Variance
Variance = 
First Quartile (lower quartile)
First Quartile (Q1) = (lower quartile) = the middle of the bottom half of the scores (returns)
Or the value of the sorted series of observations (returns) having the position x = round(0.25*(N+1))
Third Quartile (higher quartile)
Third Quartile (Q3) = (higher quartile) = the middle of the top half of the scores (returns)
Or the value of the sorted series of observations (returns) having the position x = round(0.75*(N+1))
Range
Highest score (highest return) - Lowest Score (highest return)
Interquartile Range (IQR)
It’s a measure of statistical dispersion, being equal to the difference between the third and first quartiles.