Allocation Selection and the Efficient Frontier:
The Efficient Frontier graph shows the most efficient risk and return combinations from different asset allocations. Graphically, the efficient frontier is a line that describes the most efficient tradeoff between investment risk and return. Each point along the line is an optimal combination of risk and returns: the most return the investor can get with a given level of risk, or the least risk that the investor has to bear with a given return.
This optimal tradeoff of risk and return is achieved through diversification, where the imperfect correlation among different asset classes helps decrease the standard deviation of the overall portfolio. After the efficient frontier has been derived, combining it with the investor’s preference gives us one optimal asset allocation for a specific investor.
Optimization:
If we assume that all asset returns are normally distributed, we can describe these assets with their first and second moments, namely, their expected returns, standard deviation, and correlations among each other.
Mathematically, the efficient frontier is derived from maximizing expected return with boundary conditions:
subject to 
where 
represents the weights used to aggregate different assets into one portfolio, 
is the expected return vector of assets, and 
is the variance-covariance matrix of different assets.
The solution to this optimization problem is:
(1)
where 
is the Lagrange multiplier associated with the weight constraint, and 
is the Lagrange multiplier associated with the mean constraint.
With this optimal weight, the relationship between standard deviation and the expected returns of the portfolio can be described by the following equation:
(2)
Equation (2) describes the tradeoff between 
and 
. And it is a hyperbola in mean-standard deviation space as shown below:
The Efficient Frontier:
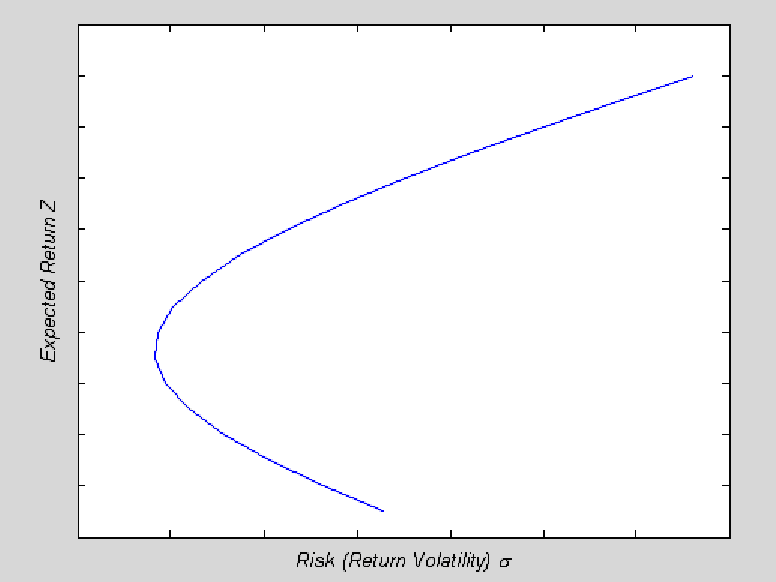
Any point below the efficient frontier represents an inferior portfolio. That is, we can increase return without incurring additional risk, or can decrease risk without sacrificing returns.
Inputs Needed:
To derive the efficient frontier, the required inputs include: the expected returns of different asset classes, the standard deviation of different asset classes, and the correlation between each pair of them.