Overview
This section provides an example of how proration for new accounts is calculated in Morningstar Office, and shows the differences between billing in arrears versus billing in advance.
Consider the following sample account whose entire value comes from three transactions:
A deposit of $100,000 of cash on 2/1/20yy
A deposit of $100,000 of cash on 2/7/20yy, and
A withdrawal of $50,000 of cash on 2/14/20yy.
How does proration work when a quarter is billed in arrears?
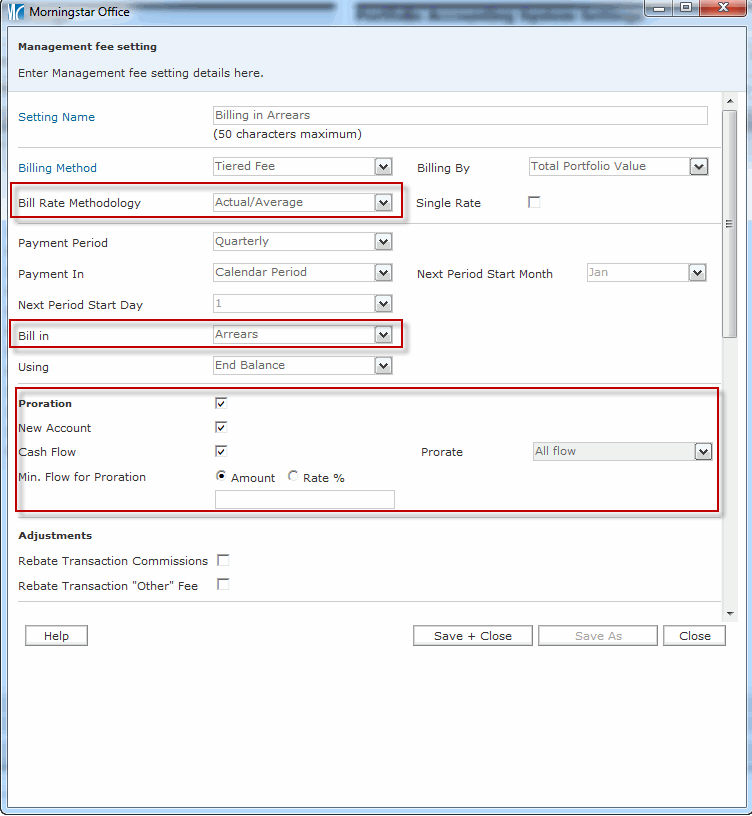
In the scenario below, note the following points about the management fee setting being used for this account:
the management fee setting is set to bill quarterly at a 1% annual fee (0.25% per quarter)
the Bill Rate Methodology for the management fee setting is set to Actual/Average
the Bill In field for the management fee setting is set to Arrears, and
the management fee setting is set for Proration for Cash Flows, and on All Flows.
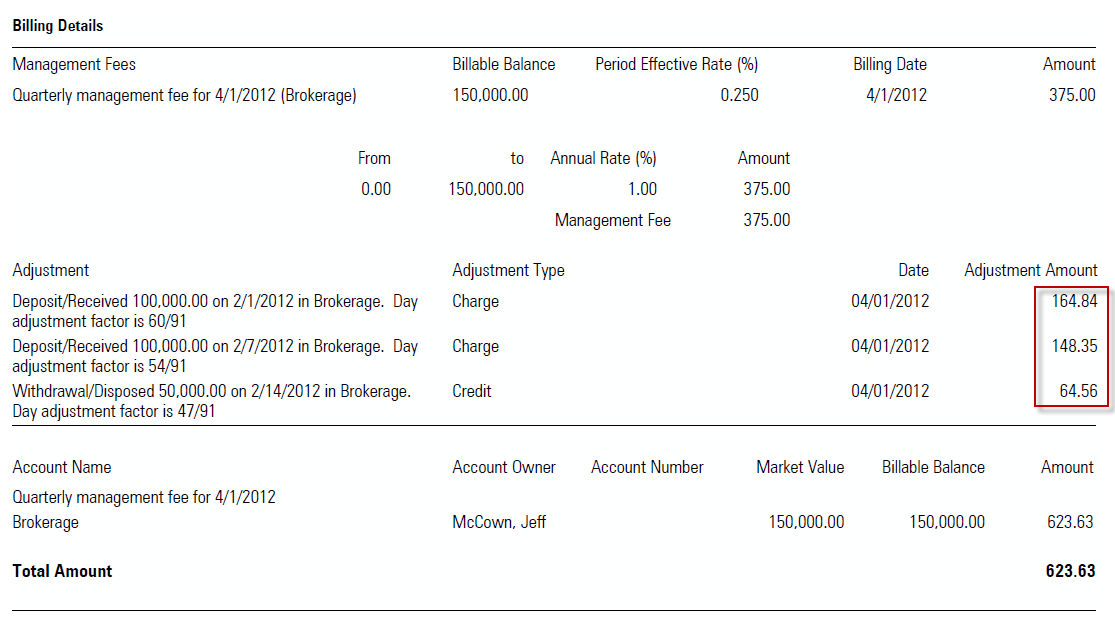
When the Billing Summary is generated for this client, the system will first calculate the fee due based on the ending value amount ($150,000), then subtract and credit back all adjustments as related to proration.
Remember our three transactions:
A deposit of $100,000 of cash on 2/1/20yy
A deposit of $100,000 of cash on 2/7/20yy, and
A withdrawal of $50,000 of cash on 2/14/20yy.
In this case, the following day adjustment periods are considered when making these calculations:
1/1-2/1 for the discrepancy between the start of the quarter and the initial deposit
1/1-2/7 for the second deposit, and
1/1-2/14 for the withdrawal.
The calculation is for each day adjustment period is:
|
A/B = C |
Where:
A = Number of days elapsed in the quarter prior to transaction
B = Number of days in the quarter
C = Day Adjustment Ratio
Note: In this case, the Bill Rate Methodology is Actual/Average, so the number of days in the (first) quarter is 91. If the Bill Rate Methodolog y had been Actual/Actual, the number of days in the quarter would also have been 91 (31+29+31), since 2012 was a leap year.
In this case, the day adjustment ratio for the first deposit on 2/1 is:
|
31/91 = 0.340659 |
The value for the day adjustment ratio for the second deposit is:
|
37/91 = 0.406593 |
The value for the day adjustment ratio for the withdrawal is:
|
44/91 = 0483516 |
Next, the following formula is used:
|
(C x D) x E = F |
Where:
C = Day Adjustment Ratio
D = Quarterly Rate (from the management fee setting)
E = Value of Transaction
F = Adjustment/Credit
In this case, the credit due for the first deposit is calculated as:
|
(0.340659 x 0.0025) x 100000 = 85.16 |
The credit due for the second deposit is calculated as:
|
(0.406593 x 00.25) x 100000 = 101.65 |
The charge for the withdrawal is calculated as:
|
(0.483516 x 0.0025) x 50000 = 60.44 |
To calculate the total fees due, sum all of the credits and charges:
|
-85.16 - 101.65 + 60.44 = -126.37 |
Finally, subtract this total from the non-adjusted quarterly fee
|
15000 x 0.0025 = 375 |
to reach the fees due for this quarter.
|
375 - 126.37 = 248.63 |
How does proration work when a quarter is billed in advance?
This section explains how proration works for an account that’s billed in advance with mid-period deposits and a withdrawal prior to the first full billing quarter.
Note: To see how to immediately bill a new account in advance, see “Appendix 3: Immediately Billing New Clients in Advance” on page 87.
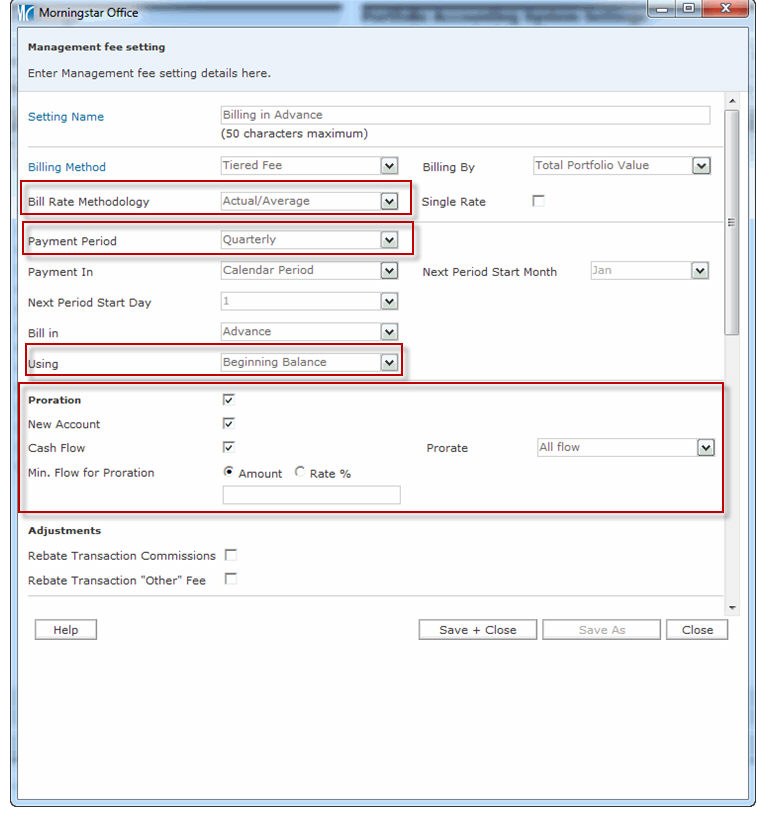
In the scenario below, note the following points about the management fee setting being used for this account:
the management fee setting is set to bill quarterly at a 1% annual fee (0.25% per quarter)
the Bill Rate Methodology for the management fee setting is set to Actual/Average
the Bill In field for the management fee setting is set to Advance, and
the management fee setting is set for Proration for Cash Flows, and on All Flows.
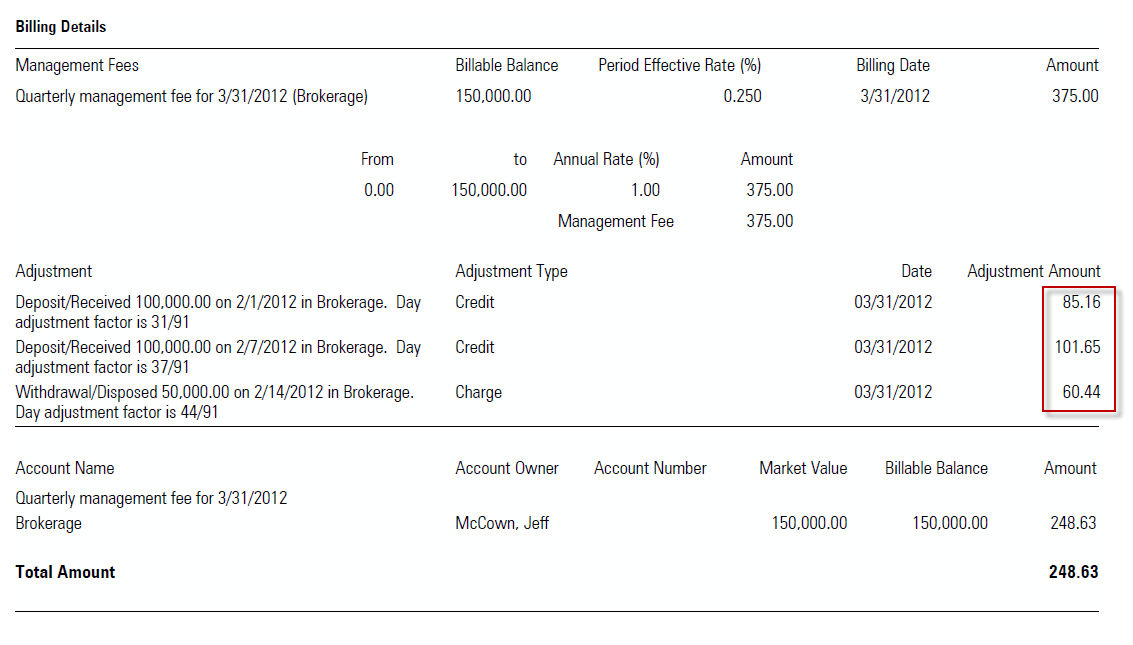
When the Billing Summary is generated for this client at the start of the second quarter, the system will first calculate the fee due based on the beginning value amount ($150,000), then subtract and credit back all adjustments as related to proration.
Remember our three transactions:
A deposit of $100,000 of cash on 2/1/20yy
A deposit of $100,000 of cash on 2/7/20yy, and
A withdrawal of $50,000 of cash on 2/14/20yy.
In this case, the following day adjustment periods are considered when making these calculations:
4/1-2/1 for the discrepancy between the start of the quarter and the initial deposit
4/1-2/7 for the second deposit, and
4/1-2/14 for the withdrawal.
The calculation is for each day adjustment period is:
|
A/B = C |
Where:
A = Number of days passed since the transaction, to the start of the current quarter
B = Number of days in the quarter
C = Day Adjustment Ratio
Note: In this case, the Bill Rate Methodology is Actual/Average, so the number of days in the (second) quarter is 91. If the Bill Rate Methodology had been Actual/Actual, the number of days in the quarter would also have been 91 (30+31+30).
In this case, the day adjustment ratio for the first deposit on 2/1 is:
|
60/91 = 0.659340 |
Note: Remember, 2012 was a leap year and had 29 days, hence the adjustment of 60 days (29+31).
The value for the day adjustment ratio for the second deposit is:
|
54/91 = 0.593406 |
The value for the day adjustment ratio for the withdrawal is:
|
47/91 = 0.516483 |
Next, the following formula is used:
|
(C x D) x E = F |
Where:
C = Day Adjustment Ratio
D = Quarterly Rate (from the management fee setting)
E = Value of Transaction
F = Adjustment/Credit
In this case, the charge for the first deposit is calculated as:
|
(0.659340 x 0.0025) x 100000 = 164.84 |
The charge for the second deposit is calculated as:
|
(0.593406 x 0.0025) x 100000 = 148.35 |
The credit due for the withdrawal is calculated as:
|
(0516483 x 0.0025) x 50000 = 64.56 |
To calculate the total fees due, sum all of the charges and credits:
|
164.84 + 148.35 + (-64.56) = 248.64 |
Finally, add this total to the non-adjusted quarterly fee already due in advance
|
150000 x 0.0025 = 375 |
to reach the fees due for this quarter.
|
375 + 248.63 = 623.63 |